The Superluminal Integral
About Integrals
In layman’s terms, an integral is defined as an integration of an infinite sum of infinitesimal objects (originally rectangles by the founders of calculus) that defines a line, surface, or space. In a more physics oriented way of describing it, integrals are used as a way of taking a continuum and defining a limited area by integrating the infinite nodes that define that area into a seamless geometric structure with quantifiable definitions. Ref: http://en.wikipedia.org/wiki/Integral
The accuracy of the calculations of an integral are based on the base object shape used to define the “pixelation” that then defines the “infinitely smooth” vector. In other words, if you were using integrals to measure the curvature of gravity in the fabric of space accurately you would need a base object that accurately defines the lattice. The work of Buckminster Fuller laid the foundation for accurately defining the lattice of space-time, but it wasn’t until the recent publication of “Quantum Gravity and The Holographic Mass” by Nassim Haramein that the specific geometry of space was confirmed. The Core Network lattice is also based on this fundamental geometry, and all possible Core Networks could be calculated using an integral equation.
Types of Integrals
There are many types of integrals, including:
- double integral
- triple integral
- contour integral
— including clockwise integral, anticlockwise integral, line integral around pole, etc - surface integral
- volume integral
- finite part integral
— also known as Hadamard regularization
and finally,
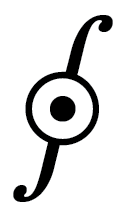
The Integral Around a Point
The “integral around a point,” or Superluminal Integral, defines any boundary curvature around a point; in other words it describes a proton around a singularity (and any of its volume layers), a planet around its core, a sun around its core, a galaxy around its black hole, etc. The “integral around a point” defines the very nature of the Universe spherically surrounding every Planck Spherical Unit in space-time.
Why we call this the Superluminal Integral
In regards to it’s Superluminality, this integral also can describe the function that is necessary to create a “boundary condition” around the center of a starship that separates the internal space-time dynamics from the external lattice. This type of boundary would enable an object to move through the quantum vacuum lattice without acceleration or warping of space, which enables Superluminal Travel (faster than light, and even instantaneous change of location). After all, neutrinos have a boundary condition which allows this!
